Getting an LLM to Set Its Own Temperature

Large language models are notoriously bad at simulating randomness.

To demonstrate this, let's try asking Microsoft's Phi-2 model (2.7B parameters) to pick a random integer between 1 and 20 (both inclusive). We'll use the following prompt and sampling parameters:

Thankfully, Phi-2 can represent all integers in our given range with a single token, so we only have to consider a single probability distribution to understand how frequently each integer within our range would be sampled. Additionally, since Phi-2 is a white-box language model, we have direct access to this probability distribution¹.

Here's what it looks like²:

Clearly, the model's output is far from uniform: some integers are chosen much more frequently than others, which is obviously not a desirable quality in a random number generator.

How would you fix this?

One (rather obvious) solution is tool use. You could ask a model with tool calling capabilities to write some Python code that uniformly samples integers from the given range. This code could be executed, and the resulting output could be formatted as a natural language response by the LLM.

But there's another, more interesting solution to this problem that occurred to me recently. If you set the LLM's temperature to positive infinity (+∞), the probability distribution becomes uniform! This has to do with how temperature scales the logits before they are passed through the softmax function. As the temperature increases, differences between logits are diminished, and in the limit as temperature approaches infinity, all possible outputs become equally likely:

Being aware of this trick is pretty valuable in this particular scenario, because it makes possible to randomly sample from a uniform distribution that the LLM generates.

But what if an end user isn't aware of this temperature scaling technique? Or, what if they dealing with an entirely different task where the "sweet spot" for temperature is non-obvious? If only there existed a tool to reason about the nature of a given prompt and come up with a suitable temperature setting for our language model...

Oh wait, an LLM can do that! Here's me asking Claude Sonnet 4 about the optimal temperature for our random number generation task:

Using structured extraction on a response like this one, you can pull out the suggested temperature value and use that to set the original LLM's temperature (i.e., the one tasked with random number generation). Better yet, you can just use a single LLM that requests to have its own temperature changed whenever it deems it necessary. To my knowledge, this blog post is the first mention of this type of technique, so I'll take the opportunity to coin a term for it: ThermoAsk³.

ThermoAsk can lead to some obvious improvements in the quality of generated responses, namely in cases where the default temperature value (typically 1.0) is not suitable for the task at hand. In such cases, it's a nifty solution for automated temperature selection.

But imagine a less contrived version of our original random number generation example where the model is actually allowed to freely generate text before it outputs the final numerical answer. In this case, we wouldn't immediately want to set the temperature to positive infinity, as we'd want the model to first generate some coherent text. Therefore, we might stick to using a lower temperature value for a majority of the response, but allow the LLM to make a tool call to adjust its own temperature right before it outputs the integer answer.

In the same vein, consider the following prompt:

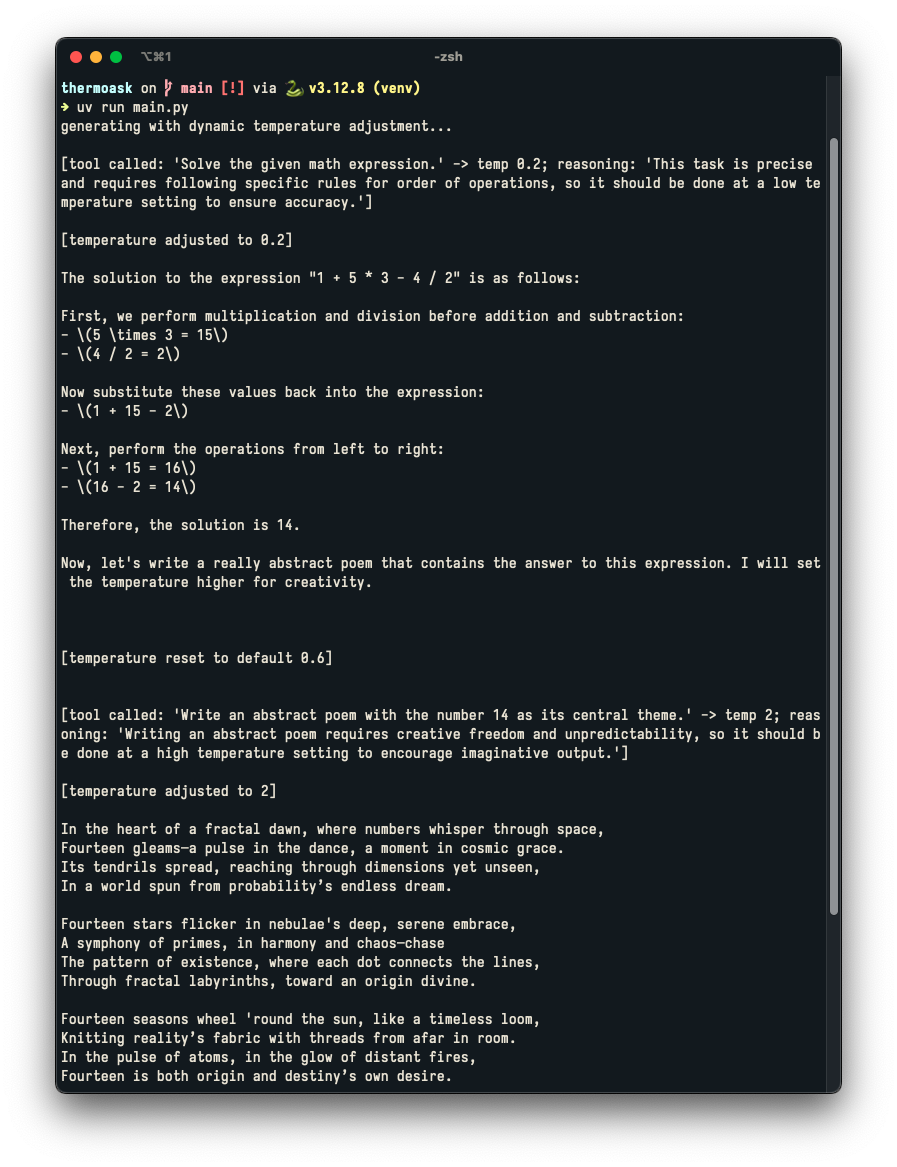
An LLM that can automatically use ThermoAsk (via tool calling) could modify its own temperature at multiple different points during generation:

I've created a simple implementation of ThermoAsk that relies on Ollama's Python SDK and Qwen2.5-7B (Phi-2 doesn't support tool calling out of the box). Try it out for yourself, and let me know what you think! For reference, here's what happened after I used the prompt above with this system:

I hope you found this blog post interesting; I'd love to hear your thoughts on it! You can reach me on X/Twitter or Bluesky, and you can also email me at amanvir.com [at] gmail [dot] com.

1. For a black-box model, you'd have to repeatedly sample from the model to approximate this distribution.
2. Well, this chart is only sort of accurate. The language model does assign non-zero probabilities to a few tokens that aren't valid integers in our range, but for our purposes, I ended up ignoring these tokens and normalizing the probabilities for all valid tokens (this is equivalent to constrained decoding for our setup). While I did explicitly specify that I only wanted an integer in the response, Phi-2 is a small model, so you can't expect too much from it at the end of the day :)
3. Although ThermoAsk is a novel idea (at least, to the best of my knowledge), the general idea of using an LLM as a sampler for another LLM has been explored before. Check out this interesting post on LessWrong, which proposes a strategy in which an LLM is asked directly to pick a token from a list of top-k tokens generated by another LLM.